art and math have the same basis: visual grammar

Art and math have the same basis.
I do not mean that art has mathematical basis as many authors have written.
My claim is that there is the same visual-grammatical basis for all the mental activities, including math and art.
The proto visual grammar is formed by experiences which enter through the visual sense organ.
To see a picture we customarily see it on perceptual level.
When we enjoy it formally however, we forget time passing and the work being a thing in space: shape seeing is not practical.
Art seeing (shape seeing) is not perceptual seeing but sensual seeing.
Any association from seeing is the secondary activity of perception.

There is a frequently quoted topic in Hermann Weyle's book "Symmetry".
When the mathematician proved that there are only seventeen ways to cover a plane with tiles artists already had used all the possible way.
Since the time of Ancient Egypt until modern time, the patterns had been used.
This suggests that the ability to make patterns is universal.
Making the pattern solved the mathematical problem, which means that applied art can solve applied mathematical problem.
Everyone can see shapes, which  teaches him  apriori self organized system of shape.

Seeing a shape is to see the quantifiable geometrical characteristics of the shape, which have number concept.
Most noticeable characteristic is countability of shape.
String, loop, dot, cavity and coil are countable elements:

Then can the proportion represent number?

Effect of the proportion in art work has been popular; especially of golden section.
I put it aside because the length of a line segment cannot be exactly measured by sight.
It is as hard as weighing a thing by holding it or hearing absolute pitch.
What the example shows is the orderly size difference of the shapes.

The proportion can be sensed exactly in this way by the help of countable squares.
The proportional element appears at the last stage of art style; there are many art works ignoring the exact proportion.

Visual sense is the most important sense organ because it can count the characteristics of shape and  grouped shapes.

Babylonia, Maya, Ancient China, and  Ancient Egypt had similar numerical system: grouped shapes represent natural number.
The notations of the small number like 1, 2, 3 are similar in all of these ancient civilizations.
The inconvenience to write large numbers made invention of sign; each civilization has different sign.
It supports the idea that the concept of number did not come first but sensing shape made the concept of number.
The representation of number concept inevitably became same everywhere.
The same shapes of the ancient numerical system is the archaeological remnant of what ancient people had before language, which suggests that the universal grammar is not language but shape.

Before learning any sign system every child self-teaches the structural relation of shape by visual experience.
Though every child masters the basic visual grammar it is usually replaced for sign system by education.
A few grown-ups do not forget the great pleasure of seeing shape to become artist or mathematician.
Clive Bell writes,
"I wonder sometimes, whether the appreciators of art and mathematical solutions are not even more closely allied. Before we feel aesthetic emotion for a combination of forms, do we not perceive intellectually the rightness and necessity of the combination?"

There is a story that Socrates could instruct an ignorant slave boy to solve a geometrical problem.
The boy had innate ability; how old could he be?
Around ten year old since he could serve as a house servant?
There is an IQ test with shapes for the lower grader of elementary school, which means that  children of younger than ten must have the ability to see the shapes in the test.
There is some evidence to lower the age further: dozens of You Tube movie about child pianists.
It seems that three year old kids are ready to learn playing the piano, which means they can understand the musical structure.

                                                         (three year old Hiyori plays)
A child player must be curious about hearing musical structure.
Then where the curiosity and ability come from?
There must be a preceding ability: the visual sense.
All the children are curious about shapes.
My guess is visual sense has innate ability of recognizing structural system of shapes.
This structural understanding becomes the model of all the mental activity: all the other abilities are moulded on this formal system.

Shape seeing is the innate ability every child can do.
But analysing three year old child's drawing cannot show us how the child's visual sense ability is; to play the piano a child does not have to create sounds since the piano prepares all the sounds;  it is like a child who can sense a circle can draw a circle using  PC.

This visual ability remind me of Chomsky's universal grammar.
"....the theory suggests that some rules of grammar are hard-wired into the brain, and manifest without being taught.
Chomsky has speculated that UG might be extremely simple and abstract, for example only a mechanism for  for combining symbols in particular way, he calls Merge. ....the human brain contains a limited set of rules for organizing languages....all languages has a common structural basis. This set of rules is known as universal grammar."(Wikipedia)

My assumption is that the set of rules can be self-taught by the experiences of seeing shapes.

I am more familiar with Piaget, so let me quote from Wikipedia about Piaget's "The Child Conception of Space".
"Children at the earliest stage, when asked to reproduce certain geometric figures, preserved only the topological features; that is, they were accurate in terms of continuity/discontinuity, enclosure/ exclusion, inside/ outside, nearness/ farness."

I use this idea as the principle to explain visual grammar.
The topological features of shapes can construct number concept and logical system: proto visual grammar appears at this stage.

there is shape relation to show us number concept: the nearness of shapes makes a group and isolate from other groups.

The grouped shapes show the number concept and such group can be arranged in order: the lower grader at elementary school can learn counting with the picture of apples.


There is another obvious relation of shapes which can teach us basic logic.
When I say we have innate logical intelligence, I mean there is logical structure of shape and our sense experience can notice it.
Kids can draw a face with two eyes, which means they understand the number 1,2 and inside- outside relation.
I call such faculty of counting and of logic proto visual grammar, which can be developed to visual grammar.

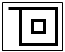
Let me show a simple logical example: the possible position of two loops( loop shown as square).
When there are two loops one is either inside or outside of the other.

To add one to the left pattern there are three possible positions: outside of the large square; between the two squares; inside the small square.

To add one to the right pattern there are two ways: outside two squares; inside the either one of the squares.

(the same pattern is shown in blue)

There are good examples in Arp's works which show his grammatical awareness.
I listed up some examples.

Arp writes,


"....I wanted to create new appearances, to extract new forms from man.
We do not wish to copy nature. 
We do not want to reproduce, we want produce.
We want produce as a plant produce a fruit and does not itself reproduce.
We want to produce directly and without meditation.
As there is not the least trace of abstraction in this art, we will call it concrete art."

His genius picked patterns from pre-existing list of shapes.

every shape is made of string

"In a black and white drawing the spaces are all white and all are bounded by black lines; in most oil paintings the spaces are multi-coloured and so are the boundaries; you cannot imagine a boundary line without any content, or a content without a boundary lines....therefore,when I speak of significant form, I mean a combination of lines and colours( counting white and black as colours)"
   (Bell "Art")
Seeing a line as a boundary line of content is perceptive seeing.
Seeing a line itself without content is sensitive seeing.
We can see an object and its two dimensional reproduction in the same way on sense level: the retinal images of both are two dimensional, which is why we can establish unified art theory for every thing we see.

 When we say that these shapes are same, it means we move the eye on both shapes in the same way.
Imagine the first one is made of string and the second of  a piece of wood.
We still can say that we see these things in the same way: we move the eye along the outline.
Seeing a shape is tactile: the finger can sense a shape along the contour.

Let me explain the eye movement using the model below: the line becoming wider and finally we see only one edge.

We can see a line because it has thickness, which means the line has two edges.
When the line is narrow both edges are seen at once which is the same as we see one edge.
When the line becomes wider we see the two edges, which is why we see the area.

Everything we see becomes a design network on the retina.
Every network is made of string.
The simplest network is a string and a closed string is a loop.
It can be said that a string is an element.
As atoms make a molecule and may become compound, string may compose more complicated patterns.

We can also start with a network as an element.
In this case a string or a loop is a broken network.
A network has countable strings and dots( meeting points of strings).
When two strings meet at a point, the result is a string.
Only when more than three strings meet at a point a dot appears
A dot is expressed as D(N), N=3,4,5....: dot with N strings.
As every design is made of string and dot, the eye counts the number of the strings and the dots when we see it.The model can be drawn on grid having the characteristics of proportion and angle.
For example D(0) type has only two models: 

Let me show some examples; there are many D(0) with two loops inside in Arp's paintings.

All the shapes belong to the same D(0) type with two loops inside:

Some of them look like creatures with two eyes, which is perception level of seeing.
Piaget wrote that young children acquire topological level of seeing at very early stage.
.I consider this is the beginning of sensitive seeing.
Associating two eyes which  consists of sensing and referring comes later.

The model works to classify alphabet:

There are ten types of models in this group.

D(0)

D(3)

2 D(3)

 D(4)

Not only the alphabet but any design has a string model.
For example using the two models above this new model can be made.

Imagine this is stretchable string then it is easy to make Arp's work bellow.

Many modern paintings originated from Cubism (including Constructivist painting, Dada ism painting) have distinctive types of string model, which suggests they belong to the same group.

"I wonder.... whether the appreciators of art and of mathematical solutions are not even more closely allied.... I have been inquiring why certain combinations of forms move us; I should not have travelled by other road had I enquired, instead, why certain combinations are perceived to be right and necessary, and why our perception of their rightness and necessity is moving."
     ( Bell)
Bell is showing which  direction I should go.

Unified art theory

I found this  image on-line recently.
My definition of art being any visually enjoyable image, this is an art work in my everyday life.
The original sculpture which is very likely to exist somewhere at this moment is as remote as a galaxy.
Art exists at the moment of seeing it.

The replica of this sculpture is the same as the original in appearance: the original work minus originality is the replica.
A free size model in any material can be made, which I call solid model.
From the model many single views can be made.
The Arp sculpture becomes reproductions, which I call flat model.
The digital image above belongs to this model.

The first prints in Western art history were produced as the reproduction of painting for public
and the oldest masterpieces of Chinese calligraphy exist only as copy.
They are considered to be art work.
Digital work is this century's reproduction and is art.

The flat model has colour and texture impression.
This model minus colour is black and white colour model.
The texture impression becomes small structure of its own as a roof can be covered with tiles.
Subtracting the tone from this model the design appears.
Now we reached what Vasari said in sixteenth century: design is the basis of all the art.

These lithographs below by Picasso belong to the same series which shows that abstract process happened within iconic level.

In the right one we can recognize a head, two horns, a body, four legs, a tail, and a male organ.
The elements of the shape are clearly recognizable: it consists of eight lines and three loops.

there are some good examples of art with totally definable geometrical characteristics in art history: Tangram; Ancient Roman letter design.

According to Wikipedia,
"The tangram is a dissection puzzle consisting of seven flat shapes, called tans, which are put together to form shapes.
The objective of the puzzle is to form a specific shape using all seven pieces, which may not overlap."
They say there are over six thousand five hundred shapes in the books published in nineteenth century.
It means that people in general can distinguish thousands of shapes easily and enjoy each of them.
I call this ability proto visual grammar.
this ability appeared as another pastime in Renaissance.

"The idea of geometrically rationalizing ancient Roman inscriptions became something of a pastime with Renaissance scholars. ....even Albrecht Durer published treatises on the subject, and the idea has been pursued, with varying amounts of success,
by artists and typographers ever since." (Wikipedia)

There is no art history but applied art history.
Pure art appeared occasionally when real artist among applied artists became aware of formal problem.
Serialists in music were very conscious of the significance of formal sound structure.
"In serialism the order of the twelve notes of the chromatic scale is determined pre-compositionally. The pitch rows are usually not repeated until the entire row has been played. However, pitches or a group of pitches can be repeated in succession. Total serialism extends the concept of serialism to rhythms, dynamics, tempos, meters and other non-pitch elements."
(Wikipedia)

Though some artists like Moholy-Nagy, Mondrian, Doesburg, Herbin, Max Bill used the formal method they were not aware of  using the same universal grammar which is like musical grammar.

Moholy-Nagy left the comment:
"In 1922, I ordered by telephone from a sign factory 5 paintings in porcelain enamel. I had the factory's colour chart before me and I sketched my paintings on graph paper. At the other end of the telephone, the factory supervisor had the same kind of paper, divided into squares. He took down the dictated shapes in the correct position. ...."(Experiment in totality)

Design with definably quantified geometrical characteristics belongs to perfect design model.
Let me start with an simple design: an ancient letter B; the type of B with two triangles attached on the right side of vertical line.

We need a line with certain thickness to draw any shape.
So I call it borrowed thickness.
All the visible geometrical characteristics are predetermined quantitatively and each characteristic is recognizable separately.
Removing one characteristic each time from the perfect design, we can conceive of the other models.

The proportion of the two triangles can be changed(proportion free model).

To recognize as B, the relative size of the two triangles should not be so different(partially proportion-free model).

The angles of the triangles can be various as long as the one side of the two triangles is aligned(partially angle-free model).

When all the angles are free the B-likeness disappears(angle free model).

A line can be curved like these:

I call this characteristic curved-ness.



These belong to the same group(curved-ness free model).

Tangram shapes are made of convexo-concave lines.

This puzzle suggests that convexo-cavity is essential to represent shape-likeness.

Without the smoothness of line, the shape can be drawn with shaky line or dotted line( smooth line free model =shape model).

Many artists used this type of line without sharpness, avoiding smooth line. Arp's relief with string is a good example.
Tapestry line and digital line are this type too.

The similarity of a triangle and a circle is being shape with no concave.
If a triangle is called a three sided polygon a circle can be called infinitely-sided polygon. These two belong to the same type of concave model.


Making a letter B with string on a sheet of paper, shake the paper a little.

It is no more readable as B but may look like two loops attached at a point.
The loops have  concavity( concave model).

Shaking further the loops loose tension and become loose strings attached at a point(string model).

Now there are seven models as total:
   Perfect model = Proportioned model
   Proportion-free model = Angled model
   Angle-free model =Curved-ness model
   Curved-ness-free model = Smooth line model
   Smooth line-free model = Shape model
   Shape-free model = Concave model
   Concave-free model = String model
Any design has these models and each model transformable to the next.
The transformation is reversible, starting from String model to Proportioned model.
The same idea can be expressed as diagram in two ways:

The ideas in my old blogs can be expressed as diagrams too.

Fine art is a sort of applied art.
Applied art is a sort of artefact
Artefact is a sort of natural object.

I see a bird drawing by Picasso(Art of code).
The bird looks like a white dove which is a symbol of peace( Art of symbol).
Without such knowledge it is still a bird(Art of icon).
With paying no attention on the semiotic content, I see the lines of the drawing(Art of form).

    Imagination is the faculty based on cognition.
    Cognition is based on perception.
    Perception is based on sense.
    To appreciate art formally only sense is necessary.

Each faculty makes its own world.
Sense makes art.
Perception makes physical world.
cognition makes real world.
imagination makes literature and religion.

C.S. Peirs says ethics is based on logic and logic is based on aesthetics.
I think aesthetics is based on visual grammar and visual grammar is based on sense.

Now I am ready to start establishing visual grammar.